详解KMP算法

KMP有那么难吗？

学计算机的朋友一定对字符串匹配的场景不陌生，比如Linux 的 Grep 命令。如何快速在一个大文本快速高效查找某一个字符串？这个时候就要用到KMP 算法了。KMP 全称为Knuth-Morris-Pratt算法，以三位发明这个算法的计算机巨佬命名的。

一般在大学《数据结构》这门课程都会介绍这个算法，我当年上学的时候也学过，但是一直没弄懂。特别是对Next 数组学的云里雾里，迷迷糊糊到大学毕业。工作几年后也没有用到这个算法，但KMP 像一根刺卡在我的脑海里，如此普遍使用又基础的一种算法，难道这辈子都不打算搞明白吗？这个算法真的有那么难吗？带着这份不甘和疑惑，我又重新学习了这个算法，认真花了两个小时终于完全弄懂了。其实KMP 并不难！关键弄懂为什么会有Next 数组？以及如何快速求解Next 数组？这两个问题想明白了，KMP 就弄懂了。

字符串匹配的过程

举个例子

给一串文本S: ababadabcbabcababacbc

要查找的串P: ababac

现在要在S 中查找P 是否存在？如果不考虑性能的话你会怎么做？可能会这样暴力匹配：首先比较 P[0,5] 与 S[0,5]，即 P[ababad] 与 S[ababac] 串，P[0] 对准S[0] 位置，比较 P[0] 和S[0] 是否相等，相等的话接着比较 P[1] 与 S[1]、P[2]与 S[2]…直到P 的末尾字符。如果都不相等的话。P 的串会整体向后滑一位，就像游标一样。接下来比较 P[0,5] 与 S[1,6] 的串是否相等, 如图所示:

KMP2

不难看到这样做的时间复杂度为 O(n*m)。仔细看下暴力匹配的过程，在P对准S[0] 位置时，会比较 P[ababac] 与S[ababad]，这两个串[0,4] 都是”ababa”，只有最后一个字符’d’ 与’c’ 不相等。

KMP1

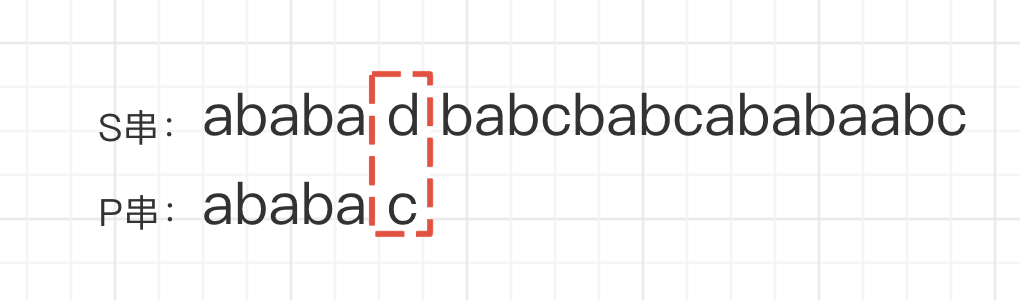
这会导致匹配失败。之后P串往后移动，对准S[1] 位置。等下！关键点就在这里，我们只能把P 串往后移动一个位置吗？经过一次匹配失败我们已经知道 P[0,4] 和 S[0,4] 是相等的，这个是付出了一定代价才拿到的信息。能否利用这个信息做些事情呢？能不能将P 串往后多移动几位而不只是一位来减少不必要匹配？当然，是可以的

先来看两个概念，前缀和后缀:

前缀：除最后一个字符外，一个字符串全部头部组合
后缀：除第一个字符串外，一个字符串全部尾部组合

拿字符串”ababa”来说，

前缀：a、ab、aba、abab.
后缀：a、ba、aba、baba

有了前缀、后缀的概念后，现在我们要去计算一个值V，这个值是前缀与后缀最长共有元素长度。对于串”ababa”来说，V的值是3，最长前缀和后缀共有元素为”aba”。有了v值后，对于匹配失败的情况

往后移动的位数 = 已经匹配串的长度-V

回到前面的例子，已经匹配了P和S中的”ababa” 串，到’c’ 与 ‘d’ 不相等失败，这个P 往后可以移动的位数为 5-3 = 2，可以跳过S[1] 位置，P[0] 直接对上S[2] 位置。这里求得的的V值其实就是P串的Next数组中Next[4] 的值。Next[i] 为P[0,i] 串中求得的前缀和后缀最长共有元素长度。不难求出对于上面的P串”ababac”的Next 数组值如下表:

Next数组	0	1	2	3	4	5
搜索串P	a	b	a	b	a	c
值	0	0	1	2	3	0

有了Next 数组，每次匹配失败后，查找串P 可以往后移动的位数不仅仅只有一位了

移动的位数为 = 已经匹配串的长度-Next[i]
i为匹配失败的下标的前一位

这样可以加快搜索效率，使得时间复杂度降到O(m+n)

通过上面我们知道了Next 数组的概念，也知道Next 数组可以帮忙提高搜索效率。但是为啥匹配失败后往后移动的最大位数是上面的公式？

KMP5

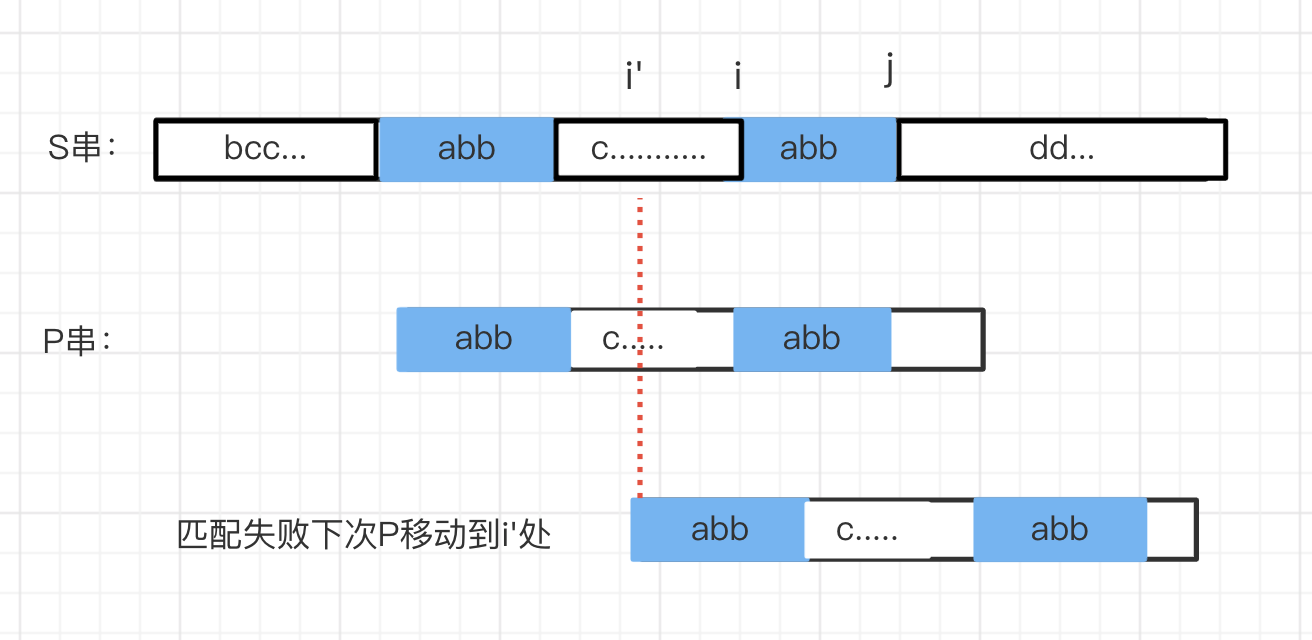
如上图，蓝色部分是P[j] 前后缀最长公共字符长度，即Next[j] 值，P 在j+1 位置因为字符相等匹配失败，下一次整个串往后移动，最大可以移动到 i 位置继续匹配。有没有可能在i 之前的一个位置i’ 上，P 能和S 发生匹配呢？

用反证法证明下，假设P可以跳到i’位置，i’< i，在i’ 位置上P 与S 完全匹配。可以看到

S[i',j] == P[i',j] == P[0,j-i']

而P[i’,j] 是 P[0,j] 的后缀，P[0, j-i’] 是 P[0,j] 的前缀，这两者相等的话，说明最大前后缀的公共长度为 j-i’，因为 i’< i， j-i’ > j-i，这就矛盾了.j-i 的值是求出的 Next[j] 值。换言知，如果i’ 存在的话，那么 i’ 一定和 i 相等。毕竟 Next 数组求的就是前后缀最长公共字符的长度。

如何求Next 数组

明白了Next 数组的意义，下面看看怎么求出 Next 数组。可以利用动态规划的思想，如果已知Next[i] 的值，怎么求Next[i+1]呢？

KMP6

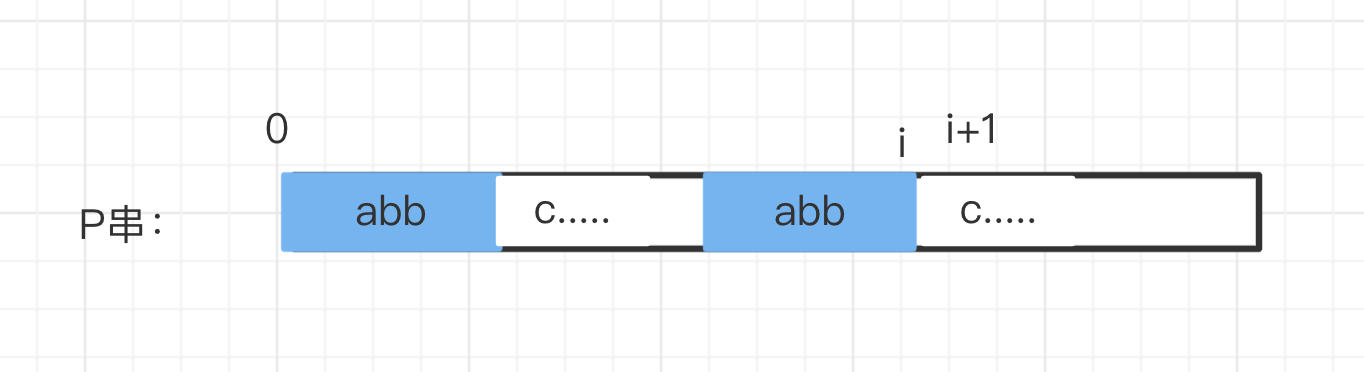
如图：P的最长前后缀公共串为”abb”，Next[i] 的值为3。如果P[i+1] == P[3] 的话，那么显然 Next[i+1]=4

if P[Next[i]] == P[i+1]:
	Next[i+1] = Next[i] + 1

如果不相等呢？

KMP7

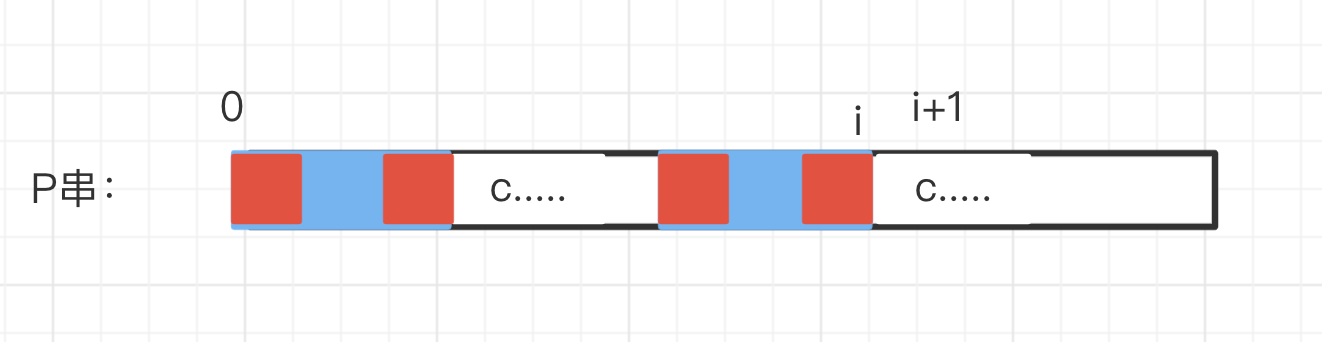
图中红色的为 Next[Next[i]] 的值，可以看到

if P[Next[i]] != P[i+1]
	递归下去比较 P[Next[Next[i]]] 与 P[i+1]

实现

看完上面的内容，搞明白了KMP 算法了吧，其实并不难，下面贴上完整的Go 实现

求Next数组：

calcMaxMatchLengths := func(s []byte) []int {
		match := make([]int, len(s))
		for i, c := 1, 0; i < len(s); i++ {
			v := s[i]
			for c > 0 && s[c] != v {
				c = match[c-1]
			}
			if s[c] == v {
				c++
			}
			match[i] = c
		}
		return match
	}

// search pattern from text, return all start positions
	kmpSearch := func(text, pattern []byte) (pos []int) {
		match := calcMaxMatchLengths(pattern)
		lenP := len(pattern)
		c := 0
		for i, v := range text {
			for c > 0 && pattern[c] != v {
				c = match[c-1]
			}
			if pattern[c] == v {
				c++
			}
			if c == lenP {
				pos = append(pos, i-lenP+1)
				c = match[c-1] // 不允许重叠时 c = 0
			}
		}
		return
	}

KMP有那么难吗？

字符串匹配的过程

如何求Next 数组

实现

CATALOG

FEATURED TAGS